Polyhedral Conic Classifiers for Visual Object Detection and Classification

Polyhedral Conic Classifiers for Visual Object Detection and Classification

摘要

我们提出了一类准线性判别式，在滑动窗口视觉目标检测和开放集合识别任务方面优于目前large-margin的方法。在这些任务中，分类问题不仅在数值上是不平衡的，即在训练和测试时正样本比负样本要少得多，而且是几何不对称的，正样本通常形成紧凑的，视觉上一致的group，而负样本更多样化，包括任何不是以目标类为中心的样本。使用训练样本来覆盖这样的负类是非常困难的，而在“open set”应用中会加倍困难，因为运行时的负类可能源于训练期间根本没见过的类别。因此需要一种判别式，其决策区域紧紧围绕在正类附近，同时还要考虑两个类重叠区域的负类情况。本文介绍了一类准线性“多面体圆锥”判别式，其正区域是L1球变形。 这些方法具有可与线性支持向量机（SVMs）相媲美的性能和运行时复杂性，并且可以使用与SVMs相关的约束二次规划从二元或仅正样本中训练它们。我们的实验表明，它们在大范围目标检测，开放集合识别和传统的闭集分类任务上明显优于线性支持向量机和现有的one-class判别式。

1、介绍

传统机器学习分类器如 large margin discriminants [^6,9,4]针对的是“闭集”场景 ¹，其类标签是互斥和详尽的，测试时看见的每一个类在训练时都是已知的。这些方法尝试把每个测试样本归为一个类，即使与任何已知的训练样本几乎没有相似之处——这样一个语义,是脆弱的,因为它忽略了离群值(无意义类的样本)和异常类(训练期间没有预见的)在测试时可能发生。相比之下,“开集”方法¹试图处理这些问题，通过拒绝不属于任何已知的训练类的测试样本。为此他们需要为每个目标类估计内围层或验证区域，以及传统的内部类决定边界。

视觉目标检测也应该受益于严格约束正类的判别式。在滑动窗口检测，识别问题是高度不对称的，因为正样本形成一个variable-but-coherent外观类，而负样本更多样化。而且数据也是高度不平衡的，在训练和测试时负样本窗口远远多于正样本窗口。因为这两个原因，专注于严格划定正类边界的判别式是有用的，而支持向量机(SVMs)等传统判别式把两个类当作是平等的、可互换的。 由于很多时候一个窗口会fail to be a positive，大部分SVM支持向量变成“hard negatives”，结合现有的特性集不难发现，在特征空间里这些完全环绕正类周围(投影类密度的散点图[^15,28])。 在实际应用中需要可靠的、可伸缩的、不对称的判别式，专注于将正类建模为一个紧凑、连贯的集合，其被迥异的负类海洋所包围。不这样做的陷阱如图1中所示。

这是一个在运行时出现未预见类的识别问题，但目标检测器面临类似问题，即未知的困难负样本。本文介绍了一系列准线性判别式来实现这些目标，通过使用基于通过L1锥的线性截面多面体决策边界。通过为正类提供更严格的边界，这几何结构系统地优于基于half-space的决策规则，比如线性支持向量机，在开集识别问题和检测不可预见的困难负样本问题。实际上即使在传统的闭集问题上它也通常会提高性能。训练表述为和线性支持向量机一样的高效凸优化问题，运行时间也类似于线性支持向量机。

图1：由SVM返回的决策超平面成功分隔了其训练类别（狗：正、人：负）。然而它也将奇异类的实例归类为狗类，如猫、马、鱼和椅子，有时甚至比狗自己的置信得分更高。问题在于过大的接受域——支持向量机试图分隔狗和人，而不是限制狗类的边界。一个紧密的决策边界(如多面体或椭圆体)改进了定位，减少不可预见的类和离群值造成的错误分类。

相关工作

最近的研究介绍了几项判别式或检测器，它们放弃了对称的二进制分类框架，采用了旨在为正类提供更严格建模的损失函数。通常这些被称为“one class”的方法，因为他们中的大多数可以只从正样本中学习一个类，尽管负样本(如果可用的)通常可以被合并来帮助改进决策边界。 比如Support Vector Data Description (SVDD)²试图找到一个紧凑的超平面，它包含了大部分正样本，而Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM) ³则寻找一个拟合正类的超平面，并且尽可能远地回避将负样本。其他类型的best-fitting-hyperplane分类器在[^18,5,2]中提出。Cevikalp和Triggs⁴使用一个级联凸模型分类器来逐步地从宽广的负样本海洋中切出紧凑、连贯的正样本区域，用于人脸和行人检测。其他方法比如Additive Kernels⁵和Random features ⁶试图近似于设置为固定复杂度的kernel classifiers，通过显式地将样本映射到高维空间，从而提供了非线性的类分离，从而限制了正类区域。

The name “one class” emphasizes the methods’ origins in density modeling, but it is a misnomer in that negative samples usually can be, often are, and in some formulations must be included during training.

另一种策略是由Dundar等⁷的结直肠癌检测器⁷，通过联合优化一组超平面分类器来学习多面体的接受域，每一种都被设计用来分类正样本以及对应负样本的子群。然而因为需要分割负样本集合，对于大规模问题耗费巨大，并且如果负样本集不能自然地分割成定义良好的簇，那么它也是不确定的，特别是当整体性能对分区的数量和详细结构都很敏感时。还有其他几种方法同于构建多面体来近似框出正类[^13,14,1,21,24]，但是这些方法要么在训练集大小上都很差，容易局部最优或过拟合，要么需要辅助聚类或标签，使得它们不适合大规模应用。与此相反，我们的方法有一个凸公式保证了全局最优解，它们能有效地扩展到大规模问题，而且它不需要将负样本聚类，并且通过使用一个鲁棒的基于边际的损失函数来防止过拟合。

2、多面体圆锥分类器

我们的分类器使用⁸的多面体圆锥函数，即通过L1圆锥的超平面截面的投影，来定义它们的接受区域。这个选择提供了一个方便的紧凑和凸起的区域形状(适用于适当的权重)区域形状，用于区分较广的消极类。它自然允许鲁棒的基于边缘的学习，自由参数的数量保持适度，从而控制过拟合和运行时间。

多面体圆锥函数以及扩展多面体圆锥函数分别表示为：

$$\begin{gather}\int_{\mathbf w,\gamma,c,b}(\mathbf x)=\mathbf w^\top(\mathbf x-c)+\gamma\parallel{\mathbf x-c}\parallel_1-b\tag{PCF}\\\int_{\mathbf w,\gamma,c,b}(\mathbf x)=\mathbf w^\top(\mathbf x-c)+\gamma^\top\mid{\mathbf x-c}\mid-b\tag{EPCF}\end{gather}$$

这里$\mathbf x\in{\rm I\!R}^{d}$ 是一个测试点，$c\in{\rm I\!R}^{d}$ 是锥顶点，$\mathbf w\in{\rm I\!R}^{d}$ 是一个权重向量而$b$ 是偏移。对于PCF，$\parallel{\mathbf u}\parallel_1=\sum^d_{i=1}\mid{u_i}\mid$ 表示向量$L_1$ 的范数，而$\gamma$ 是对应的权重。对于EPCF，$\mid{\mathbf u}\mid=(\mid{u_1}\mid,...,\mid{u_d}\mid)^\top$ 表示 分量模量，而$\gamma\in{\rm I\!R}^{d}$ 是对应的权重向量。

我们的多面体圆锥分类器使用了这种形式的函数，决策域$f(\mathbf x)<0$表示正类，而$f(\mathbf x)>0$ 表示负类。相似的，我们的基于边界的训练方法令$f(\mathbf x)\leq-1$ 对应正类而$f(\mathbf x)\geq+1$ 对应负类。在这两种情况下，正类区域本质上都是穿过锥点为$c$ 的 $L_1$ 锥的超截面，特别是区域$\mathbf x\in{\rm I\!R}^{d}$，即超平面$z=\mathbf w^\top(\mathbf x-c)-b$ 放在$L_1$锥 $z=\gamma\parallel{\mathbf x-c}\parallel_1$ (PCF)上所围起来的区域，或者是对角缩放了的$L_1$锥$z=\gamma^\top\mid{\mathbf x-c}\mid=\parallel{diag(\gamma)(\mathbf x-c)}\parallel_1$ (EPCF)。如图2所示。

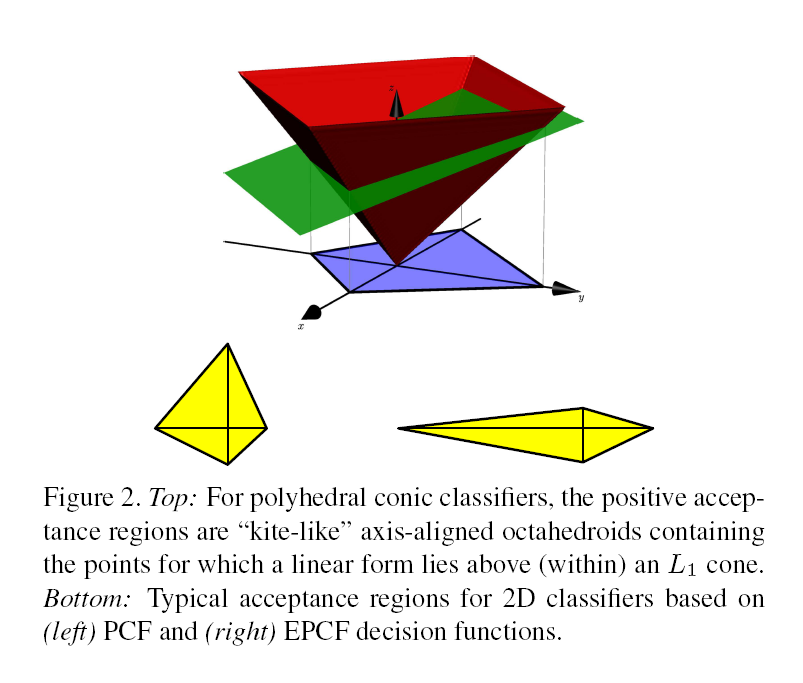
注意对于PCF，当$b>0,\gamma>0，\parallel\mathbf w\parallel_\infty<\gamma$ (其中$\parallel\mathbf u\parallel_\infty=\max^d_{i=1}\mid{u_i}\mid$ 是$\infty$ 范数)以及任何$\tau$ ，区域$f(\mathbf x)\leq\tau$ 是凸的并且在${\rm I\!R}^{d}$内是紧凑的，它包含了顶点$\mathbf c$。 类似的，对于EPCF，当$b>0,\gamma>0,\parallel w_i\parallel<\gamma_i, i=1,...,d$ 以及任何$\tau$ ，区域$f(\mathbf x)\leq\tau$ 也是凸的并且在${\rm I\!R}^{d}$内是紧凑的，它也包含了顶点$\mathbf c$。在训练过程中执行这些不等式是直截了当的，但目前我们只是简单地让决策区域自由地拟合训练数据：毕竟紧凑的正类自然倾向于产生紧凑的接受区域。

在几何上，在上述约束条件下产生的区域是有限的八面体（2d空间），其沿着从顶点$\mathbf c$开始的每个正负坐标半轴。 连接相对顶点的线段因此在c处相交，得到变形但仍然轴对齐的八面体“风筝”形状的区域，其整体尺寸由b控制。 在EPCF中，区域宽度可以沿每个轴独立地缩放，而在PCF中它们被耦合在一起，但是更有限形式的各向异性仍然是可能的。

为了在输入特征向量$\mathbf x$上定义基于边缘的分类器，对于PCF，我们把特征向量扩大为$\tilde{\mathbf x}\equiv\left(\begin{array}{c}x-c\\ \parallel x-c\parallel_1\end{array}\right)\in{\rm I\!R}^{d+1}$，权重向量扩大为$\tilde{\mathbf w}\equiv\left(\begin{array}{c}-\mathbf w\\-\gamma\end{array}\right)\in{\rm I\!R}^{d+1}$，然后令$\tilde{b}=b$。这样PCF的决策函数就与线性SVM有着相似的公式，对于正类$\tilde{\mathbf w}^\top\tilde{\mathbf x}+\tilde{b}>0$而对于负类$\tilde{\mathbf w}^\top\tilde{\mathbf x}+\tilde{b}<0$。类似的，对于EPCF我们把特征向量扩大为$\tilde{\mathbf x}\equiv\left(\begin{array}{c}x-c\\ \mid x-c\mid\end{array}\right)\in{\rm I\!R}^{2d}$，权重向量扩大为$\tilde{\mathbf w}\equiv\left(\begin{array}{c}-\mathbf w\\-\gamma\end{array}\right)\in{\rm I\!R}^{2d}$，然后令$\tilde{b}=b$，同样的得到与线性SVM有着相似的公式，对于正类$\tilde{\mathbf w}^\top\tilde{\mathbf x}+\tilde{b}>0$而对于负类$\tilde{\mathbf w}^\top\tilde{\mathbf x}+\tilde{b}<0$，不过现在是在2d维度。对于PCF和EPCF上下$\mp1$的边界可以转成相似的$\mp1$的SVM边界，使得我们可以使用标准SVM最大边界训练算法的软件。因此便可以在增广的特征向量上运行相似的SVM二次方程程序：

$$\begin{align*}&\arg\min\limits_{\tilde{\mathbf w},\tilde{b}}\frac{1}{2}\tilde{\mathbf w}^\top\tilde{\mathbf w}+C+\sum\limits_i\xi_i+C\_\sum_j\xi_j\\& \begin{array}{r@{\quad}r@{}l@{\quad}l}s.t.&\tilde{\mathbf w}^\top\tilde{\mathbf x}_i+\tilde{b}+\xi_i\geq+1, i\in\it I_+,\\&\tilde{\mathbf w}^\top\tilde{\mathbf x}_j+\tilde{b}-\xi_i\leq-1, i\in\it I_-,\\&\xi_i,\xi_j\geq0,\end{array}\end{align*}$$

其中$\it I_\pm$是正负训练样本的索引集合，

将PCF和EPCF特征向量插入到上述训练过程中分别给出了我们的多面体圆锥体分类器（PCC）和扩展多面体圆锥体分类器（EPCC）方法。 请注意，尽管它们表面上呈线性对称形式，但这些分类器本质上是不对称的：它们强制正面位于内部，负面位于外面，多面体的圆锥形区域通常紧凑并以正面为中心。 我们的公式对于过拟合是强大的，并且可以使用标准的SVM技术，如切面法[12]和快速原始空间求解器（例如[30]），因此可以很好地扩展。

3、实验

我们在合成以及真实数据集上测试了提出的多面体圆锥分类器，还有开放集合识别以及传统的闭集多类判别。作为对照我们报告了其他几种线性与非线性方法的结果，包括SVM,1-Sided Best Fitting Hyperplane Classifier (1S-BFHC)⁹,GEPSVM ³, one-class SVM (SVDD) ², 以及Additive Kernels method⁵。更进一步地，我们测试了使用第二多项式核函数的Kernel SVM(KSVM)。对于开集识别问题，我们也比较了所提出的方法与1-vs-Set Machine method ¹。我们没有与⁷中的多面体方法作比较因为那个源代码弄不到。

我们强调的是，我们的多面体分类器最好被认为是线性支持向量机的替代选择，它们在测试中系统地表现优异，无论是应用还是使用的特征，只少量增加内存使用和运行时间。Kernel SVMs和类似的基于实例的方法通常会有更好的绝对精度，但是它们通常在实际应用中运行非常缓慢，除非作为级联分类器的最后阶段，然后早期阶段使用比较快的方法，比如我们的方法。训练时也是这样：在下面的人脸检测实验中，最终训练集大小大约有250k， kernel SVM算法比如Sequential Minimal Optimization¹⁰难以处理这种规模的数据集。由于这个原因，在对象检测测试中包含了kernelized 方法的结果是不实际的。但是我们测试了一种近似于kernelized 方法的 Additive Kernels method⁵。为了评估性能，我们报告分类率或PASCAL VOC式的平均精度(AP)分数¹¹。对于多类问题，我们使用了一个one-against-rest(OAR)公式，因为它对所有方法都适用。

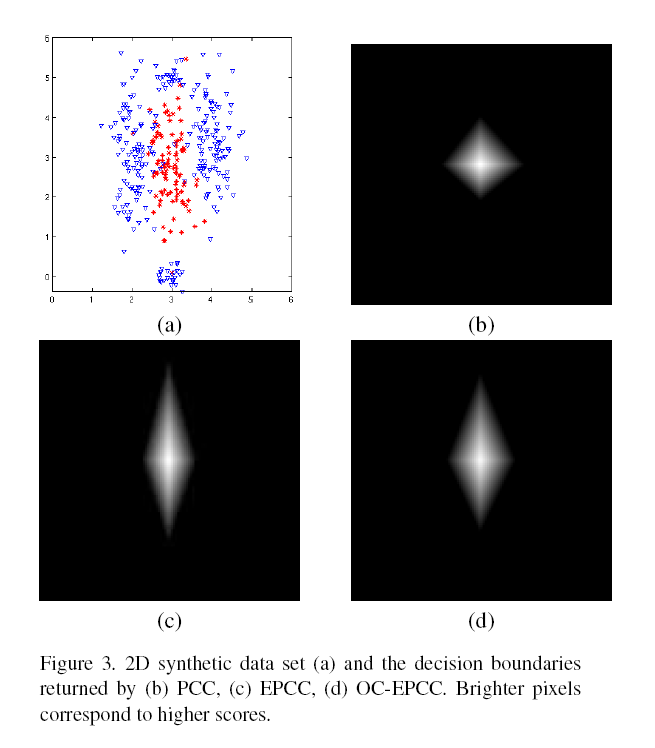
3.1合成数据说明

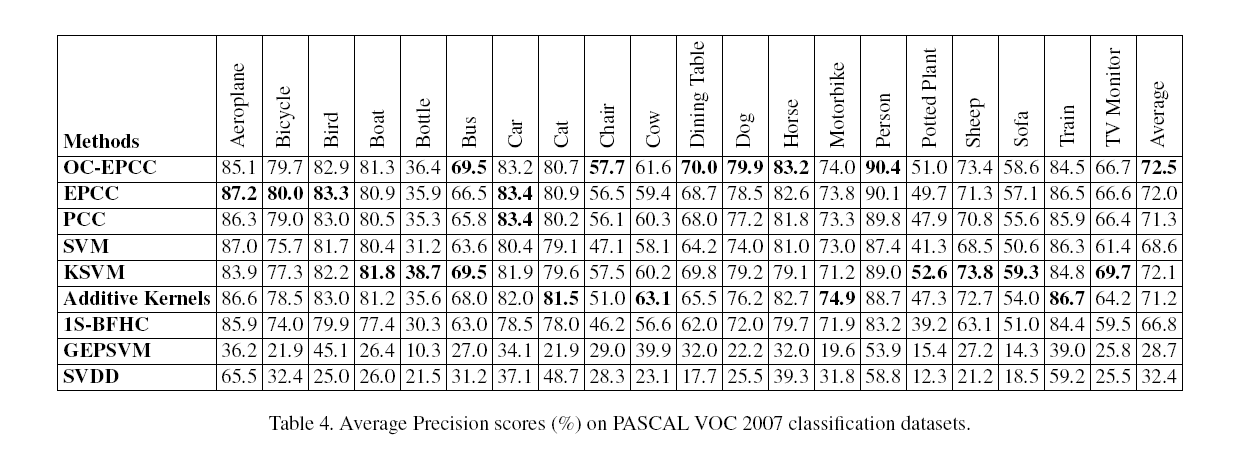
图3说明了该多面体圆锥分类器在合成二维数据集上的结果，其包含的正类随机点高斯均值为$\left(\begin{array}{c}3\\ 3\end{array}\right)$以及axis-aligned标准差为$\left(\begin{array}{c}0.1\\ 0.9\end{array}\right)$，而负类是一个标准差相同的混合高斯模型，均值是在正类附近的几个值。从数据上来说，表1给出了从这些分布取样的250个正样本/ 750个负样本组成的测试集的经验平均精度。准确度最好的是statistically-optimal Bayes分类器，其次是EPCC。One-class EPCC(OC- EPCC)也做得很好，即使在这里测试的版本是单独使用正样本进行训练的。线性支持向量机表现很差，因为该问题不是线性可分的。一种将数据显式映射到18维特征空间的Additive Kernel method做得更好，但不如我们的方法只需要使用3维或4维嵌入。

3.2对象检测实验

3.2.1人脸检测试验

为了便于对方法进行直接比较，我们训练了数个完全相同的滑窗人脸检测器，使用(准)线性分类器的除外，对所提出的PCC和EPCC方法进行了测试，对[5]中的1S-BFHC hyperplane-fitting分类器、线性SVM和Additive Kernels也进行了测试。在训练中，我们使用了2万个从网上收集的正面垂直的脸的图像。对于负样本集，我们从相同图像的没有脸的区域随机抽取了10000个有复杂的背景的窗口。子图象是缩放和裁剪到尺寸35×28然后表示为620维LBP+HOG特征向量。请注意，就像经常在人脸检测中那样，需要有比特征维度远远多的正训练样本。

为了允许部分侧面姿势的变化，我们使用频谱聚类将正训练样本分成三组，并在每个组上训练出给定类型的单独分类器。每一个初始的检测器被用来扫描一组成千上万的图像集合来收集困难负样本，而分类器被重新训练以创建最终的检测器。训练集的最终大小约为250k。采用标准滑动窗口方法¹²进行测试，将检测器窗口横向移动3个像素，垂直移动4个像素，缩放设置为1.15，使用贪婪的非极大抑制。

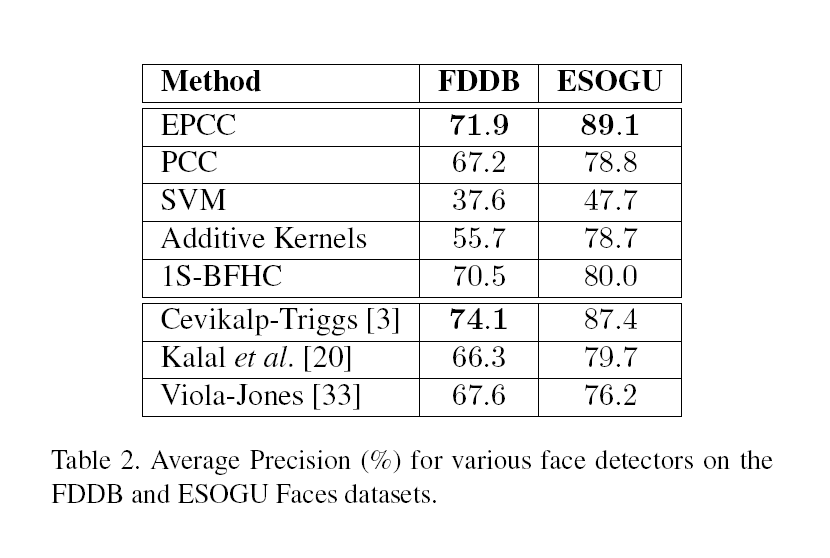
我们在两个数据集上测试了生成的检测器，包含2845图像的人脸检测数据集和基准(FDDB)¹³，以及ESOGU Faces¹⁴，其中包括667个高分辨率彩色图像，有2042个带注释的正脸。这两种方法都包括大范围的不同的图像位置和尺度，复杂的背景，遮挡和光照变化。

表2给出了上述检测器和三个公开检测器的平均预测得分，三个公开检测器分别是：

• the boosted frontal face detector of Kalal et al. ¹⁵,
• the short cascade of Cevikalp & Triggs ⁴,
• the OpenCV Viola-Jones detector¹⁶

后面几个检测器的得分严格来说并不是可比较的，因为他们使用了不同的、非公开的训练集，而且是多stages级联、final stage是非线性的，而我们的检测器只使用了一个线性stage。然而，我们提出的EPCC方法还是在ESOGU也是排第二上取得了最好的成绩，且在FDDB上取得了仅次于Cevikalp & Triggs的成绩，而Cevikalp & Triggs在ESOGU也是排第二。剩下的单一stage方法，1S-BFHC在两个数据集上都排第三，紧接着是PCC，而SVM排最后，表明简单的half-space接受域在这里是不适合的，正类需要被更紧密地包围住才能达到好效果。（EPCC、PCC和1S-BFHC都将其限制在一个有限区域内）。Additive Kernels提供了非线性决策边界，相对于线性SVM有显著的改进，但是其准确率还是低于所提出的方法以及1S-BFHC，表明其在限制正类区域方面还是没有它们做得好。

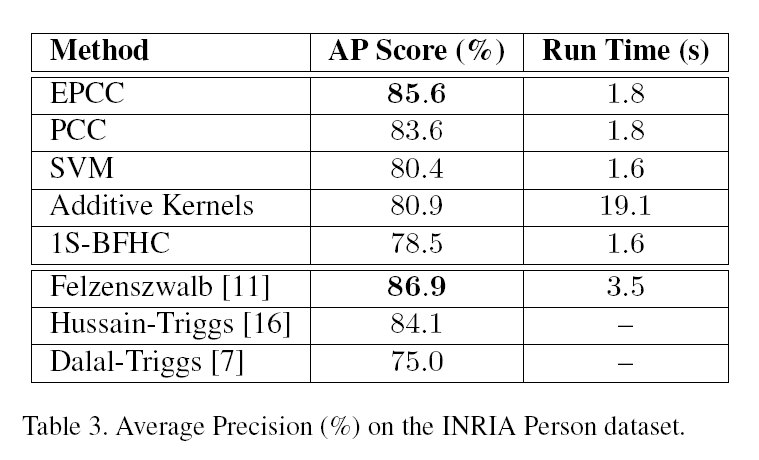
###3.3.2行人检测实验 我们在INRIA数据集上训练和测试了一系列类似的检测器，包括线性EPCC、PCC、1S-BFHC、SVM和Additive Kernels，他们的设置完全相同。我们使用了潜在的训练方法Felzenszwalb[11]，训练一对对称的不含部件的root。这对root通过对镜像图片对应用K-means聚类来初始化。我们使用了HOG特征¹² ，pixel cell为8 * 8而窗口步长为8像素，而金字塔尺度间隔系数1.07。作为对比我们引用了Felzenszwalb¹² 的公开结果（线性SVM以及HOG特征，使用一对对称的root，每个有8个组件-总共18个过滤器，以及bbox预测）Hussain & Triggs¹⁷ (一个基于线性与二次方两阶段级联的单根隐性SVM，使用了HOG+LBP+LTP特征)，以及Dalal & Triggs¹⁸ (只使用HOG特征的简单的线性SVM检测器，没有latency, multiple roots 或 parts)。

表3实验结果准确率以及每张图片的测试时间。EPCC检测器在这些检测器中表现最好。因为它缺少部件（part）所以它不如Felzenszwalb多root、多部件检测器的得分高，但是它比Hussain & Triggs效果要好，尽管后者拥有更好的特征以及两阶段级联等隐含优势。PCC在这里也表现的不错。注意除了它们在准确率上的表现，EPCC和PCC的运行时间也与线性SVM很接近（只有Felzenszwalb¹² 的一半）。所以在这里EPCC是线性SVM非常理想的替代选择。对比人脸检测实验的结果，Additive Kernels只相比线性SVM提高了一点准确率但是它却是最慢的方法。

3.3 视觉对象分类实验

3.3.1 在PASCALVOC 2017上的实验

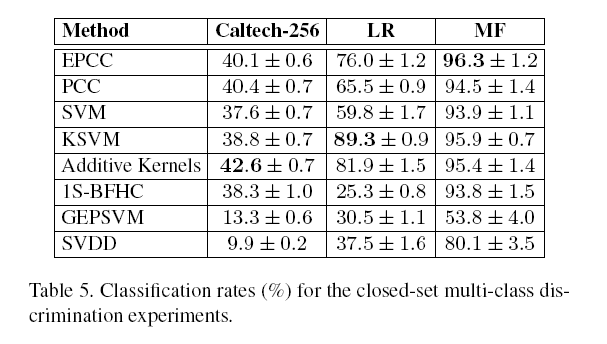
3.3.2 在多类分类数据集上的实验

3.4 在开放集合识别上的实验

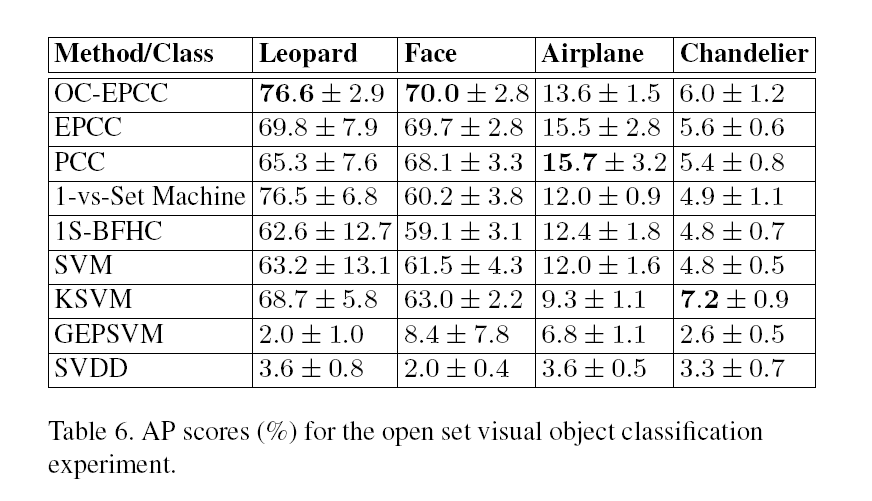
3.4.1 开放集合视觉对象分类

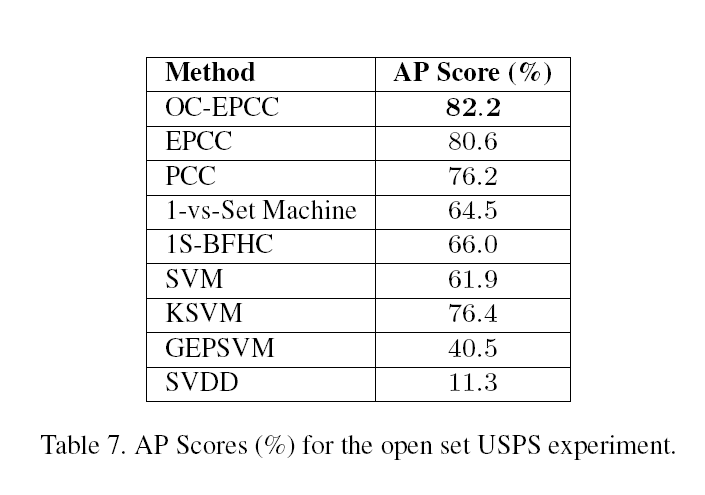
3.4.2 开放集合USPS数字识别

4、总结归纳

本研究认为，在开放集合对象识别和滑窗对象检测问题中，使用非对称分类器是有益的，将重点放在为正类(目标对象)生成紧凑、受约束的决策区域。为此，我们提出了PCC、EPCC和OC-EPCC，这是一个鲁棒的可扩展的最大边缘学习方法的家族，其正类接受区域是通过L1锥的平面截面。通过适当的参数设置，这些方法给出紧凑的、凸的接受区域，严格限制正类的范围。一个特征向量展开允许PCC和EPCC使用标准的线性SVM软件进行训练，而OC-EPCC目前使用一种类似的随机梯度下降法进行训练。我们对这些方法进行了大量的对象检测、开放集合识别和经典的闭集识别任务的测试。检测和开放集识别结果是尤为突出的，在整个棋盘上相对于类似的(准-)线性分类器都有显著的改进包括SVMs和几个单类方法。总的来说，我们相信我们的方法能够替代许多当前的视觉对象检测和分类任务中使用的像SVMs这样的线性判别式。

作为未来的工作，我们注意到我们的公式并不局限于多面体接受区域。任何其他的范式——甚至是任意的凸函数——都可以用来代替L1范式。例如,使用unsquared L2范数$\parallel\cdot\parallel$构造增广向量,$\tilde{\mathbf x}\equiv\left(\begin{array}{c}x-c\\ \parallel x-c\parallel\end{array}\right)\in{\rm I\!R}^{d+1}$，会给PCC类的分类器返回椭圆形决定区域，这是完全不同的结构,，并可能比现有的“one-class $\parallel\cdot\parallel^2$方法”如SVDD更健壮。

关于范数的补充说明

下图展示的是 二维空间范数等于1的向量集合：

引用

1. W. J. Scheirer, A. Rocha, A. Sapkota, and T. E. Boult. Towards open set recognition. IEEE Transactions on PAMI, 35:1757–1772, 2013. ↩ ↩² ↩³

2. D. M. J. Tax and R. P. W. Duin. Support vector data description. Machine Learning, 54:45–66, 2004. ↩ ↩²

3. O. L. Mangasarian and E. W. Wild. Multisurface proximal support vcetor machine classification via generalized eigenvalues. IEEE Transactions on Pattern Analysis and Machine Intelliegence, 28:69–74, 2006. ↩ ↩²

4. H. Cevikalp and B. Triggs. Efficient object detection using cascades of nearest convex model classifiers. In CVPR, 2012. ↩ ↩²

5. A. Vedaldi and A. Zisserman. Efficient additive kernels via explicit feature maps. IEEE Transactions on Pattern Analysis and Machine Intelligence, 34:480–492, 2012. ↩ ↩² ↩³

6. A. Rahimi and B. Recht. Random features for large-scale kernel machines. In NIPS, 2007. ↩

7. M. M. Dundar, M.Wolf, S. Lakare, M. Salganicoff, and V. C. Raykar. Polyhedral classifier for target detection: A case study: Colorectal cancer. In International Conference on Machine Learning, 2008. ↩ ↩² ↩³

8. R. N. Gasimov and G. Ozturk. Separation via polyhedral conic functions. Optimization Methods and Software, 21:527–540, 2006. ↩

9. H. Cevikalp, B. Triggs, and V. Franc. Face and landmark detection by using cascade of classifiers. In IEEE International Conference on Automatic Face and Gesture Recognition, 2013. ↩

10. J. C. Platt. Fast training of support vector machines using sequential minimal optimization, 1998. Advances in Kernel Methods-Support Vector Learning, Cambridge, MA, MIT Press. ↩

11. M. Everingham, L. Van Gool, C. Williams, J. Winn, and A. Zisserman. The PASCAL Visual Object Classes Challenge. Int. J. Computer Vision, 88(2):303–338, 2010. ↩

12. P. Felzenszwalb, R. B. Girshick, D. McAllester, and D. Ramanan. Object detection with discriminatively trained part based models. IEEE T-PAMI, 32(9), Sept. 2010. ↩ ↩² ↩³ ↩⁴

13. V. Jain and E. Learned-Miller. Fddb: A benchmark for face detection in unconstrained settings. Technical Report UMCS-2010-009, University of Massachusetts, Amherst, 2010. ↩

14. H. Cevikalp and B. Triggs. Hyperdisk based large margin classifier. Pattern Recognition, 46:1523–1531, 2013. ↩

15. Z. Kalal, J. Matas, and K. Mikolajczyk. Weighted sampling for large-scale boosting. In BMVC, 2008. ↩

16. P. Viola and M. J. Jones. Robust real-time face detection. IJCV, 57(2):137–154, 2004. ↩

17. S. Hussain and B. Triggs. Feature sets and dimensionality reduction for visual object detection. In BMVC, 2010. ↩

18. N. Dalal and B. Triggs. Histograms of oriented gradients for human detection. In CVPR, 2005. ↩